VDRC have developed and implemented an algorithm which constructs Euclidean Voronoi diagram for spheres in 3-dimensional space by tracing Voronoi edges. Once such a Voronoi diagram is constructed, various spatial queries can be answered most efficiently and exactly. Shown in the following figure is a snapshot of such Voronoi diagram in our software developed

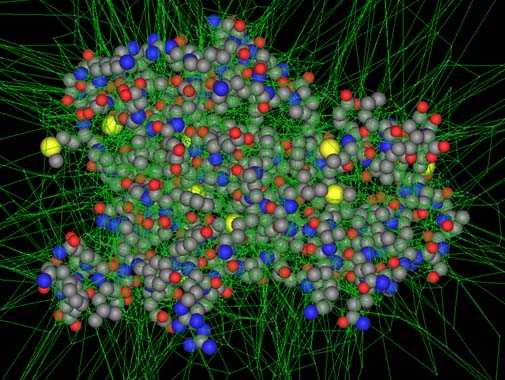
Sphere set Voronoi Diagram

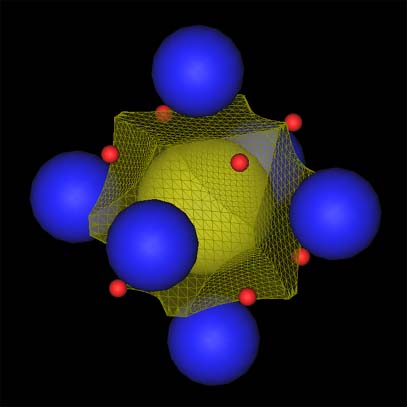
Voronoi faces for sphere set

This Voronoi diagram can be a useful tool to analyze the structural properties of proteins, and therefore we have developed and included various algorithms using the Voronoi diagram in our software for the purpose of analyzing protein structure such as defining protein-protein interface, finding largest empty space, constructing molecular surface, etc.

Seperating faces of atoms into two different groups

Internal voids

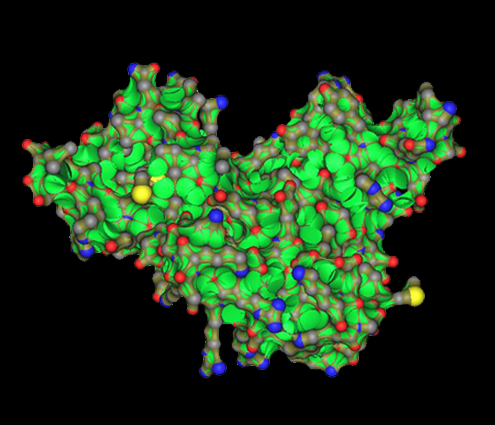
Blending surfaces

In 2001, VDRC have published a pair of papers in Computer Aided Geometric Design journal, discussing an algorithm to compute Euclidean Voronoi diagram for circles. Shown in the following figure are examples computed from our algorithm. The algorithm is based on an exact computation paradigm and takes advantage of edge-flipping based on the solution of Apollonius 10th problem. They have shown that the algorithm can compute the desired Voronoi diagram in O(N2) without failure. In the middle of the development, the famous Apollonius 10th Problem (a problem to compute circles tangent to three circles) was also solved via Möbius mapping between complex planes.

Circle set Voronoi diagram

The Voronoi diagram for circles can be applied to various geometric problems such as cable packing problem, shortest path problem, and widest channel problem.

Cable packing problem

Shortest path problem

Largest channel problem